Ch1.Wave Motion(3)- 중첩의 원칙, 복소수 표현법, 3차원 파동방정식

---

중첩의 원칙

파동은 liner system이다.
이는 두 파동의 합은 단순한 위치와 시간에서의 합으로 이루어진다는 뜻이다.

$$wave1 \ \ \ \frac{\partial ^2 \psi_{1}}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \psi_{1}}{\partial t^2} \\\\ wave2 \ \ \ \frac{\partial ^2 \psi_{2}}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 \psi_{2}}{\partial t^2} \\\\ wave1 + wave2 \ \ \ \frac{\partial ^2 (\psi_{1}+\psi_{2})}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 (\psi_{1}+\psi_{2})}{\partial t^2} \\\\$$

그러나 두 파동의 위상에 따라 합의 결과가 달라질 수 있다.
이를 간섭(Interference)라 하며, 두 파동이 합하여 진폭이 증가할 경우 보강 간섭(In-Phase), 진폭이 감소한 경우 상쇄 간섭(Out-of-Phase)라 한다.

복소수 표현법(phasor)

위상이 다른 두 조화파의 합은 복소수 표현법을 이용하여 쉽게 계산할 수 있다.

$$\psi=A\sin (kx-\omega t +epsilon^{'})\\\\ \psi=A\cos (\omega t -kx +epsilon)\\\\ e^{i \theta}=\cos \theta +i\sin\theta \\\\ \psi(x,t)=Re[Ae^{i(\omega t-kx+\epsilon)}]=Re[Ae^{i\theta}]$$

복소수로 표현된 파동은 복소수의 실수부만이 물리적인 의미를 가지므로
편의상 파동을 $Ae^{i(\omega t-kx+\epsilon)}=Ae^{i \phi}$로 표현하기도 하며 다음과 같이 phasor형태로 파동을 표기할 수 있다.

$$A\angle\phi\\\\ A\angle(-kx+\epsilon)=Ae^{i(-kx+\epsilon)}$$

이러한 방식으로 표현하는 경우 대게 $\omega t$가 생략되는 경우이며, $-\omega t$가 생략되어 표현된 경우도 있으니 주의하여야 한다.

3차원 파동방정식

1차원 파동방정식은 x와 t에 대하여 파동을 나타낸 것이다.
3차원 파동방정식의 경우 x,y,z,t에 대하여 파동을 나타내며, 이에 따라 벡터의 개념이 사용된다.

위치벡터

특정 시간 t대한 파동의 위치를 위치벡터라 한다.
(x,y,z)의 위치에 대해 $ \overrightarrow{r}=x\widehat{i}+y\widehat{j}+z\widehat{k}$의 위치벡터로 표현할 수 있다.

파수 벡터(Propagation Vector)

파동의 진행방향을 각 성분으로 표시한 벡터이다.
$\overrightarrow{k}=k_{x}\widehat{i}+k_{y}\widehat{j}+k_{z}\widehat{k}$로 파동의 진행방향을 표현할 수 있다.
파수 벡터는 전파 상수의 3차원 확장이다.
파수 벡터는 각 축으로부터의 각도에 의하여 방향이 결정된다.

파면(Wavefront)

파면은 같은 위상의 점들을 이어 만든 면이다.
1차원 파동에서 주어진 시간에 대해 파동을 선으로 표현하였듯 3차원 파동에서는 주어진 시간에 대해 파동을 면으로서 표현할 수 있다.

평면파(plane wave)

평면파는 파면이 항상 평면인 파동을 뜻한다.
평면파는 진폭이 일정하고 Propagation vector와 수직인 면의 위치벡터가 같은 위상을 갖는다.

$$\psi(\overrightarrow{r},t)=Ae^{i(\overrightarrow{k} \cdot \overrightarrow{r} \mp \omega t)} \\\\ \psi(\overrightarrow{r})=Ae^{i\overrightarrow{k} \cdot \overrightarrow{r}} \\\\ \psi(x,y,z)=Ae^{i(k_{x}x+k_{y}y+k_{z}z )}$$

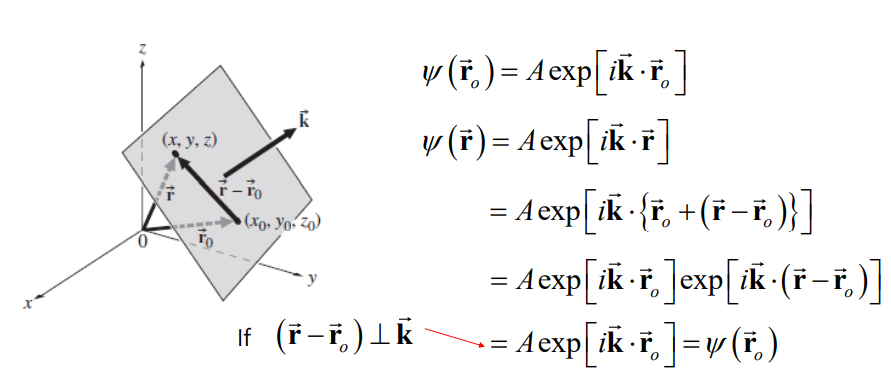
평면파의 3차원 미분방정식

1차원에서 편미분을 이용하여 파동방정식을 나타내었다.
같은 방식으로 3차원 평면파의 미분방정식을 이끌어낼 수 있다.

$$\psi = Ae^{j\overrightarrow{k} \cdot \overrightarrow{r}}=Ae^{j(\overrightarrow{k} \cdot \overrightarrow{r}-\omega t)}=Ae^{j(k_{x}x+k_{y}y+k_{z}z)} \\\\ \triangledown^2 \psi = -(k_{x}^2+k_{y}^2+k_{z}^2)Ae^{j(k_{x}x+k_{y}y+k_{z}z)} \\\\ \frac{\partial^2 \psi}{\partial t^2}=(-\omega^2)Ae^{j(k_{x}x+k_{y}y+k_{z}z)} \\\\ \omega = 2\pi \nu, \frac{\omega^2}{v^2}=\frac{2\pi \nu}{v}^2=\frac{2\pi \nu}{\nu \lambda}=\frac{2\pi}{\lambda}=k^2\\\\ \therefore \triangledown^2 \psi=\frac{1}{v^2} \frac{\partial^2 \psi}{\partial t^2} \ \ \ (\triangledown^2 = (\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}))$$

구면파(Spherical waves)

구면파는 파면이 구를 이루는 파동이다.
파면이 구면이므로 구면파는 진행할수록 거리에 반비례하여 진폭이 감소하며 아래의 파동방정식을 갖는다.

$$\psi (\overrightarrow{r})=\frac{A}{r}e^{ikr}$$